La función exponencial, es conocida formalmente como la función real ex, donde e es el número de Euler, aproximadamente 2.71828.; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.
En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma
siendo a, K ∈ R números reales, con a > 0, a ≠ 1. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen
La función exponencial ex puede ser definida de diversas maneras equivalentes entre sí, como una serie infinita o bien como un límite de una sucesión. En particular puede ser definida como una serie de potencias:
Propiedades
La función exponencial (y exponenciales en base distinta a e) satisfacen las siguientes propiedades generales.- Son las únicas funciones que son igual a su derivada (multiplicada por una constante, en el caso de que tengan una base distinta a e)
Derivada
La importancia de las funciones exponenciales en matemática y ciencias radica principalmente de las propiedades de su derivada. En particular,- La pendiente del gráfico en cualquier punto es la altura de la función en ese punto.
- La razón de aumento de la función en x es igual al valor de la función en x.
- La función es solución de la ecuación diferencial
.2
 .
.EJERCICIOS RESUELTOS
Dadas las siguientes funciones, estudia todas sus características e indica sus asíntotas. Representa su gráfica.
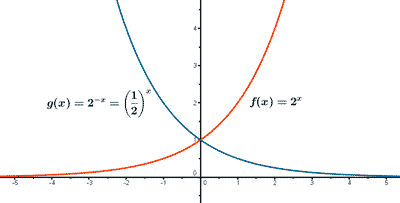
f(x) = 2x g(x) = 2 - x = (1/2)x
1) Dominio:
El dominio de las funciones exponenciales es R.
Dom(f) = Dom(g) = R .
2) Recorrido:
El recorrido de las funciones exponenciales es (0, + ∞) .
Im(f) = Im(g) = (0, + ∞) .
3) Puntos de corte:
f(0) = 20 = 1 , el punto de corte con el eje Y es (0, 1).
g(0) = - 20 = 1 , el punto de corte con el eje Y es (0, 1).
La funciones f(x) y g(x) no cortan al eje X.
4) Crecimiento y decrecimiento:
La función f(x) es creciente ya que a > 1 .
La función g(x) es decreciente ya que 0 < a < 1 .
5) Concavidad y convexidad:
Las funciones f(x) y g(x) son concavas.
6) Asíntotas:
Las funciones f(x) y g(x) tienen una asintota en el eje X.
El dominio de las funciones exponenciales es R.
Dom(f) = Dom(g) = R .
2) Recorrido:
El recorrido de las funciones exponenciales es (0, + ∞) .
Im(f) = Im(g) = (0, + ∞) .
3) Puntos de corte:
f(0) = 20 = 1 , el punto de corte con el eje Y es (0, 1).
g(0) = - 20 = 1 , el punto de corte con el eje Y es (0, 1).
La funciones f(x) y g(x) no cortan al eje X.
4) Crecimiento y decrecimiento:
La función f(x) es creciente ya que a > 1 .
La función g(x) es decreciente ya que 0 < a < 1 .
5) Concavidad y convexidad:
Las funciones f(x) y g(x) son concavas.
6) Asíntotas:
Las funciones f(x) y g(x) tienen una asintota en el eje X.
7) Tabla de valores:
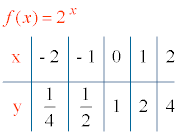
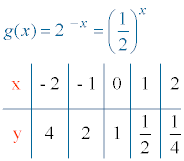
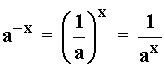
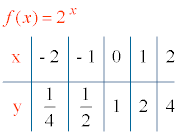
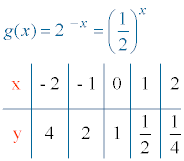

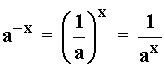
2. Dada la siguiente función, estudia todas sus características e indica sus asíntotas. Representa su gráfica.
f(x) = ex
1) Dominio:
El dominio de las funciones exponenciales es R.
Dom(f) = R .
2) Recorrido:
El recorrido de las funciones exponenciales es (0, + ∞) .
Im(f) = (0, + ∞) .
3) Puntos de corte:
f(0) = e0 = 1 , el punto de corte con el eje Y es (0, 1).
La función f(x) no corta al eje X.
4) Crecimiento y decrecimiento:
La función f(x) es creciente ya que e > 1 .
5) Concavidad y convexidad:
Las función f(x) es concava.
6) Asíntotas:
Las función f(x) tiene una asintota en el eje X.
7) Tabla de valores:El dominio de las funciones exponenciales es R.
Dom(f) = R .
2) Recorrido:
El recorrido de las funciones exponenciales es (0, + ∞) .
Im(f) = (0, + ∞) .
3) Puntos de corte:
f(0) = e0 = 1 , el punto de corte con el eje Y es (0, 1).
La función f(x) no corta al eje X.
4) Crecimiento y decrecimiento:
La función f(x) es creciente ya que e > 1 .
5) Concavidad y convexidad:
Las función f(x) es concava.
6) Asíntotas:
Las función f(x) tiene una asintota en el eje X.
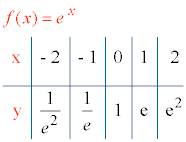
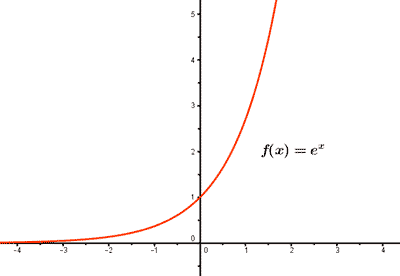
3. Dada la siguiente función, estudia todas sus características e indica sus asíntotas. Representa su gráfica.










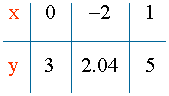
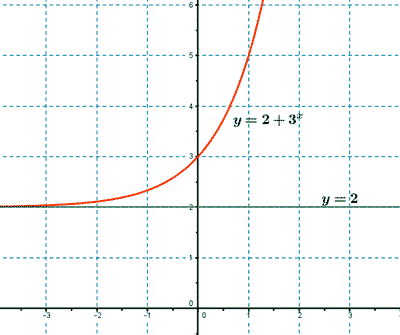
No hay comentarios:
Publicar un comentario